 This week, I'm doing a blog post to explain my approach to solving last week's Free LSAT Logic Game | Grouping: Selection (Defined).
This week, I'm doing a blog post to explain my approach to solving last week's Free LSAT Logic Game | Grouping: Selection (Defined).Again, here are the categories and topics:
P - ABE
R - HLO
W - STY
I'd put a "1-" next to each category because of the rule that we have to have at least one from each category. "1-" indicates that there's "at least one" from each, but we don't know the maximum number of variables we can have from each, so I'm not "closing" the range.
P - ABE - 1-
R - HLO - 1-
W - STY - 1-
Main Diagram
I'd draw it on paper like this:
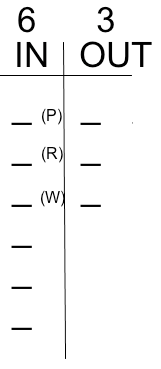
I put a P, R, and W in parentheses to the side of three of the "in" slots because we know "at least one from each category is in." It just makes that rule a bit more concrete and visual by reserving a slot for everything we know so far.
However, it's just easier to type horizontally (and some of you read this on mobiles that can't see picture files, so whenever you see a diagram I've typed, just think of it being draw vertically):
6 In: _ _ _ _ _ _
3 Out: _ _ _
1st Indented Rule:
If S is in, E and L are out.Contrapositive: If E or L is in, S is out.
Summary:
S <--+--> E
S <--+--> L
That's a "double-not" arrow. It means that at least one of the things on either side of the arrow CANNOT be in. Looking at the S-E double-not arrow (in isolation), it means that:
(1) S is out
OR
(2) E is out
OR
(3) S and E are both out.
Same goes for the S-L double-not arrow.
We can summarize the two double-not arrows as:
S <--+--> E, L
2nd Indented Rule:
If L is out, Y is in.Contrapositive: If Y is out, L is in.
Summary:
(1) Y is in
OR
(2) L is in
OR
(3) Y and L are both in.
See Conditional Reasoning for an explanation of this type or rule (and the double-not arrow, as well).
By combining the 1st and 2nd indented rules, we can form the chain:

At this point, we should think something along the lines of, "Wow, that S is pretty powerful stuff. Let's see what happens when I place it 'in'. "
Putting S "in" means E and L are "out," and Y is "in" (we inferred from that conditional chain I just made, above):
6 In: S Y _ _ _ _
3 Out: E L _
That's all we can do with S right now, but let's look at the...
3rd indented rule:
At least one topic on war will not be selected.This means we'll always have either 1 or 2 war topics "in", but never all 3. At this point, I'd draw a "(W)" to the side of one "out" slot, just to reserve it for a War topic.
(Remember: we can't have 0 war topics "in" because we always have to have at least one topic from each category "in.")
Here are the categories and topics from before, but I'd now add in the number of topics we can have from each category:
P - ABE - 1-3
R - HLO - 1-3
W - STY - 1-2
***
If we JUMP back to that little "S-in" diagram we made just a moment ago...
6 In: S Y _ _ _ _
3 Out: E L _
we'll see that we already have 2 Ws "in" (S and Y are both from the War category).
Because we can't have all 3 Wars from this category, T will have to be "out".
6 In: S Y _ _ _ _
3 Out: E L T
If we now have 3 "out", and 6 have to be "in" total, this means that everyone but E, L, and T has to be "in." Our "S-in" diagram is now complete, giving us:
6 In: S Y A B H O
3 Out: E L T
I'd write this off to the side and circle "S" to indicate that "S-in" is what started everything.
I'd then make another main diagram with S "out" and leave all the other slots blank.
***
I'm not going to explain ALL the questions because that just spoils the fun...but I will give a hint for this type of game in general.
The 1st question is a typical "List / Acceptability" question regarding specific topics. You can solve this simply by applying the rules.
However, the 2nd, 3rd, and 4th questions refer to the general categories as well.
Once you hit the 2nd question, the reference to the religion category should make you start thinking about numerical distributions (the various combinations of numbers of variables you can select from each category).
If you're decent or better with numbers, or you think you can get better by practicing, try to list all the combinations quickly.
The War category is the most limited because you can only have 1 or 2 from that category.
If we have 1 from war, that leaves 5 remaining that we'll need to pick (6 total - 1 from War = 5).
How can we make 5?
5+0, 4+1, and 3+2
However, there's no category with 4 topics, and we need at least one topic from each category (which means having 0 "in" isn't okay), so it's either going to be 3 from Politics and 2 from Religion or 2 from Politics and 3 from Religion.
This gives us the distributions:
3 Politics, 2 Religion, 1 War
2 Politics, 3 Religion, 1 War
BUT
If we have 2 from War, that leaves 4 remaining that we'll need to pick to be "in" (6 total - 2 from War = 4)
How can we make 4?
4+0, 3+1, and 2+2.
Again, there's no category with 4 (and again, we also can't have 0 from any category "in"), so it's either going to be 3 from Politics and 1 from Religion, or 1 from Politics and 3 from Religion, or we'll have 2 from Politics and 2 from Religion:
3 Politics, 1 Religion, 2 War
1 Politics, 3 Religion, 2 War
2 Politics, 2 Religion, 2 War
Of course, you don't want to take up all that space by writing so much.
Instead, I'd write the numerical distributions like this:
P-R-W
3-2-1
2-3-1
3-1-2
1-3-2
2-2-2
(I'd write them spaced-apart without a dash, but I don't want the formatting to get messed-up here.)
Recognizing numerical distributions is good stuff, but I'm not getting a kick out of it just because it's fun.
It also helps us answer the question because it becomes obvious that only the 3P-1R-2W distribution has 1R, so we know that we'll have to have 3P and 2W.
We know that the variable S will be "out" because we already have the complete "S-in" scenario (which is 2-2-2, by the way).
If S is "out", the 2Ws "in" will be T and Y, and all 3 Ps "in" means ABE are "in"... (you can take it from here)
***
What if you're not good with numbers and don't think you can get better at them?
Then, instead of trying to list all the combinations, just start with the 2nd question's limitation, that we have exactly 1 Religion topic and figure out that specific distribution instead of taking the time to list them all.
However, it makes the game much easier if you know all of them, so it's worth practicing how to do this.
I hear you saying, "but it's not fair that I have to be good at math..."
I feel your pain. I couldn't stand precalculus or calculus, but this is just addition. It's about recognizing all the ways to get to 4 and 5.
You can do addition, can't you?
The LSAT is all about thinking of all the possibilities, not just the obvious ones.
So make your 2nd grade math teacher proud and beat everyone at craps.
Photo by wisse / CC BY-NC-ND 2.0



On the main diagram, wouldn't it be reasonable to designate one space on the "Out" side as (W)? There's a cap of two on the "In" side, after all, and it's a more intuitive way to diagram that rule.
ReplyDeleteSure. That's perfectly reasonable.
ReplyDeleteSteve,
ReplyDeleteYour 'explanation' is understandable but doesn't really illustrate how one should approach answering the questions. I know you intentionally are not answering the questions but since you are advocating your approach (say, vs Kaplan) then it would be a more useful offering if you did (isn't that the point?). Not trying to be (too) critical - love the blog!
I agree with the post above. This was a great walk-through of the set up, but doesn't teach the test taker how to attack the question, or the tools that must be employed
ReplyDeleteSteve,
ReplyDeleteHelp me with question # 6. Is D the correct answer because I don't know if I will select S or not?
If I don't select T, I could have S and Y. If I select S, then I don't have E and L. Without L, I must have Y. So I know for sure I have Y, but I'm not sure I have S. I could have neither S, E, or L.
Am I thinking the right way or in left field?
Steve:
ReplyDeleteIs there any way to attack question 6 other than working out each answer until I get to D!!... this took over 4 minutes. Had this been an actual question I would have known nothing else to do other than work them all out or skip it (probably would have chosen latter) -Meaghan
So glad I read this. I'm just learning grouping and this diagramming method is exactly the structure I need to keep everything visual and improve speed.
ReplyDeleteIsn't "B" the right answer for 6th? Because if B and T are not selected, then S and Y are selected, because they always goes together, that means E and L are not selected, and that leaves only 5 selected, that is against rules.
ReplyDeleteI am pretty sure "D" is the answer, but I agree that I need a faster way to get to it. "B" determines the selection as follows: BT are out, so two of E/L/S have to be in - so therefore has to be E & L. For the War topics, this leaves Y as the only topic which will work. List is then AEHLOY (L and Y can't both be out, but both can be in - I think that is correct).
ReplyDeleteTricky...thanks for this explanation.
DeleteShould I go over every question even if understand the game and answer all correctly? It seems redundant, but I want to do whatever is recommended.
ReplyDeleteThis is a great game! I figured out the numerical distributions based on which "w" variables were in and out. There are three main scenarios; one involves S and Y in which forces T, E and L out and forces H, O, A and B in ( a 2-2-2 numerical dist.). Second scenario involves T and Y in and S out which leaves numerical distributions of 2-3-1 with the "p" and "r" variables switching between 3 and 1. Third, T and L are in, S and Y are out which leaves numerical distributions of 1-3-2 with "p" and "r" switching between 3 and 2.
ReplyDeletethis was extremely helpful and made me get a good laugh in which I haven't been able to do for a very long time since I started studying for the LSAT! thank you Steve!!
ReplyDelete