LSAT Logic Games Explanations: PrepTest 60, Game 2

This blog post covers the second Logic Game of the June 2010 LSAT (PrepTest 60).

Don't look at these explanations until you've taken PrepTest 60 as a full-length timed exam.

Also see:

PrepTest 60 (June 2010 LSAT), Game 1 Explanation
PrepTest 60 (June 2010 LSAT), Game 3 Explanation
PrepTest 60 (June 2010 LSAT), Game 4 Explanation

Explanations for Recent LSAT Logic Games

***

The rules in this game are primarily relational, meaning they require that one variable occurs before or after another, so we're dealing with a Pure Sequencing game.

In these games, I like to build the diagram step-by-step.

In this particular game, I diagram the first rule, then connect it with the second, to form:











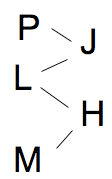
Whatever's to the left of those lines is earlier than whatever's to the right of it.

The first rule told us that L and M are earlier than H, so I've drawn lines connecting L and M to H.

The second rule told us that P and L are earlier than J, so I've reused the L that I've already drawn and placed it before J. I've also drawn a line from P to J in order to indicate that P is before J.

***

At this point, we get a conditional rule: If M is before P, then H is before G.

Since no two variables occur simultaneously, the contrapositive would simply be:

If G is before H, then P is before M.

The diagram I've previously drawn (above) is the main diagram. You can throw in a G with a slash through it to the right of the diagram if you want to deal with the conditional rule last.

However, I also like to make two big diagrams:

One with the conditional rule of: M before P ---> H before G


Another with its contrapositive: G before H ---> P before M


Initial diagram with M before P ---> H before G:








You'll notice that I placed M a bit to the left of where it previously was, just to more easily indicate that M is before P. I've also included G after H, since we know that H is before G.

However, the diagram is not yet finished because we know that G can't be last (4th rule). The only variable eligible to go last is J, so I must now create a modification of this diagram to represent that.

It becomes:




This new diagram preserves all the previous knowledge we had, but it now ensures that J goes last to avoid making G go last.

Spend at least a few moments looking at the incomplete version of this diagram (before I placed J) last to figure out how I got my final result. It's not easy, but it's important.


Diagram with G before H ---> P before M:









This one's a bit easier to make. Again, I've preserved everything we had from the combination of the first two rules, and now I've inserted G before H, as well as P before M. In this diagram, it's clear that either J or H will be last, so we've been luckier. We don't have to make any modifications to ensure that G is not last.


Quick note:

These aren't necessarily the only two possibilities, of course. It's entirely possible that neither of those conditionals will be activated (meaning the sufficient condition of either conditional statement might not be met). However, by drawing those out, we now know what happens if either of those conditionals are activated, and we also get the benefit of having a few more specific diagrams.


Now, the questions:

Question 7:

Take one rule at a time and apply it to the choices:

The first rule, that L and M go before H, eliminates choice C.

The second rule, that L and P go before J, eliminates choice A.

The fourth rule, that G goes before D, eliminates choice D.

The third rule, that M-P ---> H-G, eliminates choice B.

Answer is choice E.


Question 8:
H before G could be true in the diagram with M before P. Choice A is eliminated.

H goes 6th could be true in the diagram with G before H. Choice B is eliminated.

In the initial diagram that simply combines the first two rules, L goes before both J and H, so it can't be 5th. Choice C is our answer. (I'll go explain the remaining choices anyway).

P before M occurs in the diagram with G before H. Choice D is eliminated.

P appears second could occur in the diagram with G before H (because we could have G first). Choice E is eliminated.


Question 9:

In the initial diagram that simply combines the first two rules, we know that none of P, L, or M can go last because there's at least one variable that each must go before. We also know that G can't go last (due to the 4th rule). Looking at the diagram with M before P and at the diagram with G before H, we know that J and H could go last. Therefore, the correct answer is choice D (2).


Question 10:

This question imposes the restriction that J is before M.

Draw J - M on your paper, then, step-by-step, combine the other variables contained within the initial diagram (the one that simply combines the first two rules).

Here's one step-by-step process by which you can make all the inferences based on J going before M (the order in which you connect the variables involved in the game's first two rules doesn't really matter):




For the last step, I placed G before H simply because we know G can't be last.

Now, let's run through the choices:

GLPH works with our final product. Even though G is toward the end of the diagram, all we know about it is that it's before H. GLPH doesn't violate anything, so choice A is our answer.

I'll run through the other choices anyway:

GPHL doesn't work because L must go before H on this diagram. Choice B is eliminated.

LHGP doesn't work because G must go before H and because P must go before H. Choice C is eliminated.

LPHG doesn't work because G must go before H. Choice D is eliminated.

PLHG doesn't work because G must go before H. Choice E is eliminated.


Question 11:
If L is immediately before G, then G would occur before H (since L is before H).

When G's before H, P's before M. We've already drawn a diagram to deal with this possibility. As a refresher, it's:









Now, with the limitation that L is immediately before G, we get:








All I've done is take G from the bottom of the diagram and put it directly to the right of L.

Now, the question of what must be true:

G no later than 3rd? Well, it only has to have two things after it (H and J), so it could be 4th. Choice A is eliminated.

H appears last? Nope, J could appear last. Choice B is eliminated.

L no later than 3rd? Well, it has to have three things after it: G, J, and H, so it has to be no later than 3rd. Choice C is our answer.

I'll go through the others, anyway.

M before G? There's no rule regarding their order - all we know is that they're both before H. Choice D is eliminated.

P first? It's possible to have L first. Choice E is eliminated.


Question 12:
If M appears first...

step-by-step, place the other variables contained within the initial diagram (the one that simply combines the first two rules) after it.

We get:










Since M being first requires that M go before P, we know that H must go before G. Since G can't go last, J must go last, meaning G will go before J.

Now, the question of what must be true:

G 5th? Nope. G only has to have two things before it, so it could be as early as 3rd. Choice A is eliminated.

H 3rd? H only has to have one things before it, so it could be as early as 2nd. Choice B is eliminated.

J 6th? Yes, J must go last on our diagram, and choice C is the answer.

I'll go through the others:

L 2nd? L only has to have one thing after it (J), so it could be as late as 5th. Choice D is eliminated.

P 4th? P only has to have one thing after it (J), so it could be as late as 5th. Choice E is eliminated.


Photo by telstar