June 2010 LSAT Logic Games Explanation, Game 3

This blog post covers the third Logic Game of the June 2010 LSAT (PrepTest 60).

Don't look at these explanations until you've taken PrepTest 60 as a full-length timed exam.



Also see:

PrepTest 60 (June 2010 LSAT), Game 1 Explanation
PrepTest 60 (June 2010 LSAT), Game 2 Explanation
PrepTest 60 (June 2010 LSAT), Game 4 Explanation

Explanations for Recent LSAT Logic Games

***

This game, often referred to as "the mulch and stone game", or simply "the mulch game", was one of the tougher games of the section, simply because it only had two rules. However, you can make several inferences with these rules. I use them to make 4 main diagrams.

Initially, the rules don't give you very much to work with:







We have 7 spaces for the 7 loads. M must go on 5. We have 3M and 4S to place, and we have a maximum of (less than or equal to) 3 cleanings.

For this game, I create 4 main diagrams. All valid scenarios fall within one of the four.

I create them by taking advantage of the fact that there are only two types of variables to place in the 7 spaces: Mulch and Stone. I also take advantage of the fact that we already have a variable (Mulch) on 5.

Adjacent to Mulch on 5, we have only four possibilities:

Mulch on 4, Stone on 6
Stone on 4, Mulch on 6
Mulch on 4, Mulch on 6
Stone on 4, Stone on 6

Drawing this information on four main diagrams gives me the following:












Next to each of these diagrams, I've listed the variables that have not yet been placed (keep in mind that we have 3 Mulches and 4 Stones in total).

I draw vertical lines between consecutive variables that are different to represent the "cleanings" between different types of variables. Because the third diagram from the top only has Stones remaining to place, I completely fill in that diagram:












You can leave off here and jump into the questions and answer them all correctly. However, there are a couple of other initial inferences worth making if you can.

Both of the top two diagrams have only one Mulch remaining to place. If we placed that remaining on space 2 for both of those diagrams, they would then be surrounded by Stones. Consecutive loads of different kinds require cleanings. For the top two diagrams, placing M on space 2 results in 4 cleanings in those diagrams:













However, the maximum allowable number of cleanings is 3, so placing M on space 2 results in invalid diagrams.

(Yes, the top two diagrams in the above picture are invalid. I've simply drawn them there to show you why M cannot be on 2 in those diagrams.)

This leaves S to be on 2 in those diagrams:











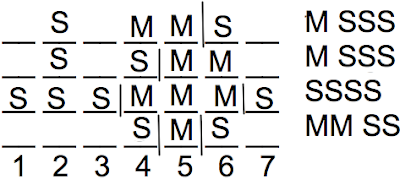
But wait - there's more. What sticks out to me at this point is that, in the 2nd diagram, we have S on both 2 and 4. Placing the final remaining M on 3 might be problematic. Let's see what happens:




Sure enough, placing M on 3 results in 4 cleanings, when the maximum allowed is 3. Therefore, having M on 3 in this diagram (the 2nd diagram in the larger scheme of things) is impossible.

Therefore, we must have S on 3 in the 2nd diagram:












Now, the bottom diagram already has two cleanings, so only one potential cleaning remains for that diagram. However, we still have 2M and 2S left to place. If we placed an M on either 3 or 7, we'd reach the limit of 3 cleanings. However, the other M would still have to touch one of the other Stones, so we'd reach at least 4 cleanings total (try it out).

Therefore, the bottom diagram can't have M on either 3 or 7, so we must have S on both 3 and 7 in that diagram:










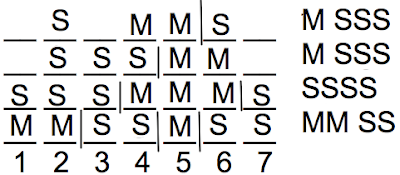
For those of you who are still reading, it's time to *finally* move on to the questions. First, a comment/caveat:

Again, I know people are going to ask me whether making all these initial inferences is really necessary. The answer is a firm "No." You can get all the questions right without doing all this work beforehand, but doing this will make the questions go more smoothly.

The method you choose depends upon your level of comfort with spending more time in the initial setup, as well as your ability to diagram quickly.

Even if you don't have the time to make all of these inferences and still have the time to get to the questions, that's ok. Again, you don't have to make all these inferences, but I still want to get you thinking about the fact that it's possible to make them. While they might give you more information than you need for these questions, it's better to have too much information than too little.


Question 13:

The best way to approach this question is to see which of the choices we've already seen happen.

Mulch on 4 and 6 occurred in the 3rd diagram, so it's our answer (choice E).

We can also eliminate all the others simply because we have a comprehensive framework for all the possible valid scenarios in the game.


Question 14:

Must the 2nd load be Stone? In our 4th diagram, we had Mulch on 2, so choice A is eliminated.

Must the 1st and 2nd loads be the same? Well, in the 1st and 2nd diagrams, it seems like they could be different. In the 2nd diagram, we could easily put Mulch on 1 and S on 7, and it would still be valid. Choice B is eliminated.

Must the 2nd and 3rd loads be different? Well, in the 2nd and 3rd diagrams, they're identical. Choice C is eliminated.

Must we have at least 2 Mulches consecutively? That occurs in all 4 diagrams, so it must be true in general. Choice D is our answer.

I'll go through the last one anyway.

Must we have at least 3 Stones consecutively? In the 4th diagram, we don't, so choice E is eliminated.


Question 15:
M on 3 could only occur in the top diagram out of the 4 main diagrams, so I'd make a more specific version of that diagram. Since there was only 1 Mulch remaining anyway, Stones will have to go in the remaining slots:





Must 6 and 7 be different? Nope, they're the same. Choice A is eliminated.

Must 1 and 2 be different? Nope, they're the same. Choice B is eliminated.

Must 7 be Mulch? Nope, it's Stone. Choice C is eliminated.

Must 6 be Mulch? Nope, it's Stone. Choice D is eliminated.

By elimination, it's Choice E (and, yes, the first load is Stone).


Question 16:

Exactly two cleanings occurs in the 3rd main diagram, as well as in our work for Question 15. We can use both of these diagrams to help us eliminate things that aren't necessarily true.

2nd load is Stone occurs in both the 3rd main diagram and in Question 15's diagram, so we can't eliminate this answer choice.

However, the only diagram (out of our 4 main diagrams) in which the 2nd load isn't Stone is be the 4th one (where we have 3 cleanings, not 2). Therefore, the 2nd load must be Stone in any diagram with 2 cleanings. Choice A is our answer.

You could pick choice A and move on, but I'll run through the other choices:

3rd load is Mulch does not occur in either the 3rd main diagram or the diagram for Question 15, so Choice B is eliminated. (Of course, seeing 3rd load being Stone in even only one of those diagrams would've been enough to eliminate it.)

3rd load is Stone occurs in both those diagrams, so we keep it for now.

6th load is Mulch does not occur in Question 15's diagram, so choice D is eliminated.

7th load is Mulch does not occur in either of those diagrams so choice E is eliminated. (Again, seeing the 7th load being Stone in even only one of those diagrams would've been enough to eliminate it.)

So, we're down to Choices A and C.

The 4th diagram isn't relevant because it has 3 cleanings. We've already used the 3rd diagram. The second diagram has Stone on both 2 and 3, so that can't possibly help us (since it wouldn't allow us to disprove either answer choice). This leaves the 1st (top) diagram.

This diagram already has the 2nd slot filled by Stone, so we know that Stone must be on 2 no matter what.


Question 17:
The 4th diagram doesn't ever have 3 loads hauled consecutively, so it's relevant to solving this question.

The 1st load is not Stone in this diagram, so we don't know whether it could be true (perhaps there's some other valid diagram where the first load is Stone and we don't have 3 loads hauled consecutively). Leave this choice alone and move on.

The 4th load is Stone in this diagram, so we know that it could be true. Choice B is our answer. Pick it, and we're done with the game.

None of the other choices occurred in the 4th diagram. (Doesn't mean they couldn't occur in some other valid diagram where we don't have 3 loads hauled consecutively, of course.)

Since the 2nd and 3rd main diagrams have 3 loads hauled consecutively, they're not relevant.

If you want to test out the other answer choices, simply take the 1st main diagram, place Stone on 3 (to avoid having 3 consecutive Mulches), then make one version of it with Stone on 1 and Mulch on 7, and make another version with Mulch on 1 and Stone on 7. You'll be able to disprove the other answer choices.

***


For more advanced test-takers, the top 2 main diagrams can be broken apart even further:

The top main diagram can be broken into 3 main diagrams based upon the 3 different potential placements of the remaining M (spaces 1, 3, and 7).

The 2nd main diagram can be broken into two main diagrams based upon the two potential placements of either the remaining M or remaining S (depending on how you want to phrase it):
















This will make the questions even easier. It's all a matter of personal preference, how much work you're willing to do up-front, and how confident you are in your ability to draw out the limited possibilities.

***

Tough game, huh?

Photo by cottergarage